해석학 공부하기

오늘도 해석학 공부를 시작하도록 하겠다. 힘들게 글들을 읽고 공부한 독자들에게는 미안하지만, 아직 진정한 해석학은 시작하지도 않았다. 그도그럴 것이, 1단원의 절반조차 마무리하지 못했기 때문이다.

그리고 장담컨대, 1단원이 제일 쉬운 단원일 것이다. 익숙한 개념들을 다시 정의하는 정도의 내용들이 대부분인 것도 그렇고, 2단원을 한 번 맛보면 정신을 못차리게 되는데, 2단원에서 배우게 되는 개념들은 해석학 내내 쓰이기 때문이다. 실제로 내가 1단원까지는 잘 따라갔지만 2단원에서 심하게 얻어맞은게 학점이 나락간 주 원인이라고 생각한다.

오늘은 왜 초장부터 이렇게 겁을 주는가 하면, 오늘 다룰 내용은 1단원 내용 중에서는 꽤 어려운 내용이 될 수 있기 때문이다. 2단원에서도 겁을 줄 계획이지만, 벌써부터 머리가 심하게 지끈거린다면 앞의 내용들을 좀 더 익숙하게 하고 오기를 바라는 마음에서 이렇게 이야기 하는 것이다. 겁주기는 그만하고, 이제 시작하도록 하겠다.

어제 내용 복습

어제는 해석학에서 첫 번째 단원인 The Real and Complex Number Systems 의 세 번째 소단원인 Fields 부분에 대해 설명하였다. 총 9개의 소단원 중 3개의 소단원을 끝낸 상태이다.

배운 내용들을 정리하자면, 실수를 구성하기 위해 field가 무엇인지 정의하고, 정의하는 과정에서 field 내부의 연산들인 addition과 multiplication 이 따라야만 하는 공리에 대해서 설명하였다.

그 다음은 연산의 정의되는 방식에 의해 field에서 성립하는 다양한 성질들에 대해 알아보았고, 그 성질들이 우리가 기존에 알던 것과 크게 다르지 않다는 사실을 확인할 수 있었다. 차이점이 있다면, 그러한 성질들이 성립하는 것이 우리가 아는 유리수라던가 실수에서만 성립하는 것이 아니라, field 이기만 하면 성립할 수 있다는 것을 배우게 된 것이다.

마지막으로, 2가지 제약조건과 함께 field 와 ordered set 의 개념을 이용하여 ordered field에 대해서 정의하였다. 여기서 기억해야 하는 사실은, 단순히 field 이면서 ordered set 이면 ordered field 인것이 아니라, 2가지 제약조건이 따라와야 한다는 것이다.

어제 내용 복습은 여기서 마무리 하도록 하겠다. 오늘은 드디어 실수체, real field 를 정의해보도록 하겠다! 그리고 정의된 실수체에서 성립하는 흥미로운 성질들에 대해 알아보고, 시간이 허락한다면 확장된 실수 체계에 대해서 알아보도록 하겠다.

The Real Field

1.19 Theorem

least-upper-bound-property 를 가지는 ordered field $\mathbb{R}$ 이 존재한다. 심지어, $\mathbb{R}$은 $\mathbb{Q}$를 subfield 로 지닌다.

해설: 드디어 $\mathbb{R}$ 기호가 등장했다! 이 기호는 보통 실수체를 나타낼 때 많이 사용되는 기호니 잘 기억해두자.

이 문장에서 말하는 것은, LUBP를 가지는 ordered field가 존재한다는 이야기이다. 여기서 한 가지 주목해야 할 부분이 있는데, 이건 ‘Definition’ (정의) 가 아니라, ‘Theorem’ (정리) 이다. 앞에서 조금 잘못 말한 부분이 있는데, 우리가 한 것은 ‘실수체의 정의’ 가 아니라, ‘실수체가 존재한다는 정리’ 에 대해서 이야기 한 것이다.

이 정리를 증명하는 것이, 이번 소단원의 Appendix (부록) 부분에서 다루는 내용이다. 조금 내용이 까다롭고 어렵기 때문에 오늘은 이걸 일단 받아들이고 넘어가도록 하자. Appendix 부록을 다루는 날에 증명을 하고 넘어갈테니 걱정하지 않아도 된다.

두 번째 문장을 보면, $\mathbb{R}$이 $\mathbb{Q}$를 subfield로 가진다고 되어있는데, subset이라는 단어는 이미 아는 단어지만, subfield 라는 단어는 처음보는 단어라 혼란스러울 수 있다. 다행히도 책에서 설명을 해두었는데 의미는 다음과 같다

$\mathbb{Q}\subset\mathbb{R}$ 이면서,
$\mathbb{R}$에서 정의된 addition과 multiplication을 $\mathbb{Q}$의 원소들에 대해서 적용한 결과가 $\mathbb{Q}$ 내부적으로 정의된 연산의 결과와 일치하고,
양의 유리수는 $\mathbb{R}$의 positive 한 원소들이다.

1.20 Theorem

만약 $x \in \mathbb{R}$, $y \in \mathbb{R}$ 이고 $x > 0$ 이라면, 아래 문장을 만족하는 양의 정수 $n$이 존재한다.

\[nx > y\]
만약 $x \in \mathbb{R}$, $y \in \mathbb{R}$ 이고 $x < y$ 이라면, $x < p < y$인 유리수 $p \in \mathbb{Q}$ 가 존재한다.

해설

여기서 이야기 한 두 정리는 불리는 특별한 방식이 있다. 첫 번째 정리는 archimedean property (아르키메데스 성질) 이라는 이름을 가지고 있고, 두 번째 정리는 특별히 이름이 있는지는 잘 모르겠지만, “$\mathbb{Q}$ is dense in $\mathbb{R}$” ($\mathbb{Q}$ 는 $\mathbb{R}$에서 조밀하다) 라고 표현되기도 한다.

우선 아르키메데스 성질에 대해 살펴보자. 이 문장에서 말하는 바는, 실수체에 존재하는 어떤 positive 한 $x$와 아무 $y$를 들고와도, 어떤 양의 정수 $n$을 $x$에 곱해서 $y$보다 크게 만들 수 있다는 말이다. 예를 들면, $x$로 $3$으로 잡고, $y$를 $10000$ 으로 잡아도, $x$에다가 $n=3334$를 곱해주면, $nx=10002>y=10000$이 되어 식을 만족한다. 증명은 아래와 같다.

archimedean property 증명

증명을 하기 위한 방식으로 귀류법을 이용하도록 하겠다. 우선 결론을 부정하여, $nx \leq y$ 라고 하자. 이 식은 모든 양의 정수 $n$에 대하여 성립하는데, 어떤 집합 $A$가 모든 $nx$들의 집합이라고 하자. $A$의 원소인 $nx$들은 모두 $nx \in \mathbb{R}$ 이므로, $A \subset \mathbb{R}$ 이고, $A$의 모든 원소 $nx$에 대하여 $a \leq y$가 성립하므로 $y$는 $A$의 upper bound 이다. 여기까지는 익숙한 개념들을 사용하여 얻어낼 수 있는 정보들이다.

여기서 우리는 $\mathbb{R}$이 LUBP를 가진다는 사실을 기억해야 한다. 앞서 이야기 한 것 처럼 $A \subset \mathbb{R}$ 이고 ($y$에 의해) bounded above 되어 있으므로, $A$는 supremum을 가지게 된다. 이 supremum을 $\alpha = \sup A$로 나타내자.

우리의 가정에 의해 $x > 0$이므로, $-x < 0$ 이고, $-x + \alpha = \alpha + (-x) = \alpha - x < \alpha$ 이다. 우리는 여기서 $\alpha$가 $A$의 supremum 이라는 점을 상기하며, supremum의 정의에 따라, $\alpha - x$는 $A$의 upper bound가 아니게 된다.

이 말은, 어떤 양의 정수 $m$이 존재해서 $\alpha - x < mx$를 만족시킨다는 의미가 된다. 이 부등식의 양변에 $x$를 더해주면, $\alpha < mx + x = (m + 1)x$ 가 된다. 여기서 문제가 발생한다.

$m$이 양의 정수이면, $m + 1$도 양의 정수이다. 따라서, $(m + 1)x$도 $A$에 포함되고, supremum은 정의에 따라 upper bound 이므로, $(m + 1)x \leq \alpha$를 만족시켜야 한다. 이는 $\alpha < (m + 1)x$ 라는 사실과 정면으로 모순된다.

결론을 부정했을 때 모순점이 발생한다는 것을 보였으므로, 우리는 $nx > y$를 만족시키는 $n$이 있다는 사실을 증명하였다. $\blacksquare$

이번엔 두 번째 정리를 살펴보자. 아무 두 실수를 잡아도, 그 사이에 있는 어떤 유리수가 존재한다는 의미이다. 물론 그 두 실수가 같아서는 안된다. 이 내용은 수학에 별 관심이 없었던 사람이라면 딱히 생각해본 적이 없을 수 있는 내용일 것이다. 슬슬 우리가 당연하다고 생각했던 이외의 내용들도 나오기 시작하는 것이다! 이제 이 정리를 증명해보도록 하겠다.

"$\mathbb{Q}$ 는 $\mathbb{R}$에서 조밀하다" 증명

이 정리의 증명은 앞에서 증명한 아르키메데스 성질을 활용한다. 자세히 읽지 않았다면 의미가 무엇인지 정도는 읽고오길 바란다.

이 증명은 귀류법을 사용하지 않은 직접적인 증명이 가능하다. 따라서, 결론을 부정한다거나 모순을 찾는다거나 할 필요는 없고, 정리의 전제, 알고있는 정의나 성질들을 활용하여 증명을 진행할 것이다.

우선 $x < y$ 이므로, $x + (-x) = 0 < y + (-x) = y - x$ 이다. 여기서 archimedean property를 이용하면, $n(y-x) > 1$를 성립되게 하는 어떤 양의 정수 $n$이 존재한다. 여기서 도대체 어떻게 archimedean property를 사용했는가 하면, 원래 정리에서 $x$의 자리에 $y - x$를 넣고, $y$의 자리에 $1$을 넣으면 된다. 얻어낸 식을 조금 조작해보면, $n(y - x) = ny - nx > 1$ 이 되고, $ny - nx + nx = ny > 1 + nx$ 를 얻게 된다. 이 식은 후반에 다시 사용될 것이다.

이번에는 조금 다른 방식으로 아르키메데스 성질을 사용해보도록 하겠다. $x$를 $1$로, $y$를 $nx$로 대체하면, $m_1 > nx$를 만족시키는 양의 정수 $m_1$이 존재한다는 것을 보일 수 있고, $x$를 $1$로, $y$를 $-nx$로 대체하면, $m_2 > -nx$를 만족시키는 양의 정수 $m_2$가 존재한다는 것을 보일 수 있다. 두 번째 식을 조작하면, $m_2 + (-m_2 + nx) = (m_2 + (-m_2)) + nx = nx > + -nx + (-m_2 + nx) = -nx + (nx - m_2) = (-nx + nx) - m_2 = -m_2$ 가 되어 $-m_2 < nx$가 된다. 첫 번째 식과 함께 나열하면, $-m_2 < nx < m_1$ 이 된다.

이건 $nx$가 임의의 두 정수 $-m_2$ 와 $m_1$의 사이에 놓인다는 것을 의미하는데, $m_1$과 $m_2$는 모두 양의 정수이므로, $-m_2 \neq m_1$이다. 따라서 우리는 $m - 1 \leq nx < m$ 이면서 $-m_2 \leq m \leq m_1$ 인 어떤 정수 $m$ 을 찾을 수 있다. 갑자기 $m_1$ 이랑 $m_2$에 대해서 이야기 하다가 갑자기 $m$이 튀어나오는지 혼란스러울 수 있다. 아래 그림과 함께 설명하도록 하겠다.

$-m_2$와 $m_1$ 을 두 대의 서로를 향해 돌진하는 자동차라고 생각하고, 그 사이에 $nx$가 있다고 생각해보자. $nx$가 어떤 값이 정확히 알 수는 없지만 2가지 경우로 구분할 수 있다. $nx$가 정수인 경우와, 그렇지 않은 경우이다.

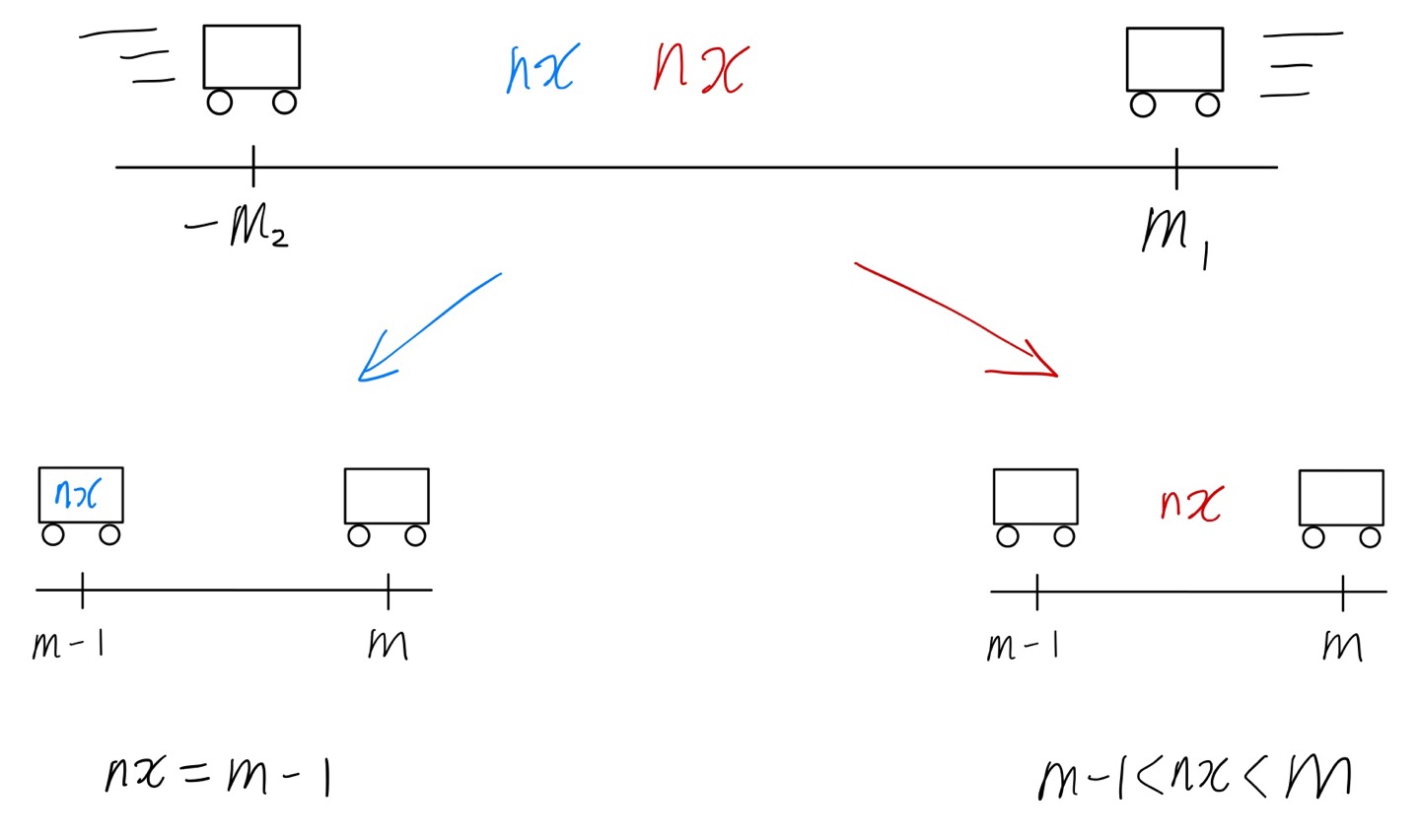
$nx$가 정수인 경우에는, $-m_2$가 $nx$가 있는 곳까지 간 뒤, 그 값을 $m-1$로 잡으면 된다. 그렇다면 $nx$는 당연히 $m$보다 작아지게 되고, $m-1 \leq nx < m$을 만족시키게 된다.

$nx$가 정수가 아닌 경우에는, 그냥 범위를 충분히 좁히다 보면, $m-1 \leq nx < m$를 만족시키는 $m$을 찾을 수 있게 된다. 참고로 두 경우 모두 $m$을 찾는 과정에서 $-m_2 \leq m \leq m_1$을 만족하게 된다.

지금까지 우리가 얻어낸 정보를 정리해보면, $ny > 1 + nx$ 를 만족시키는 어떤 양의 정수 $n$이 존재한다는 사실과, $m - 1 \leq nx < m$을 만족시키는 어떤 정수 $m$이 존재한다는 사실이다. 두 번째 식을 조금 조작해보면, $m - 1 + 1 = m \leq 1 + nx < m + 1$ 이 된다.

앞 부분을 뗴어다 보면, $m \leq 1 + nx$ 인데, 기존의 식에서는 분명 $nx < m$ 라고 되어있다. 이 두 식을 종합해보면, $nx < m \leq 1 + nx$가 된다. 그리고 우리가 맨 처음에 얻어낸 식과도 종합해보면, $$nx < m \leq 1 + nx < ny$$ 가 된다는 것을 알 수 있다. 이 식에서 $1 + nx$ 부분을 덜어내면 $nx < m < ny$가 되고, $n$의 양의 정수라는 사실을 이용하여 order를 유지한 채로 모든 식에 각각 $n$을 나누어 주면, $x < \frac{m}{n} < y$ 가 된다는 사실을 발견할 수 있다! 🥳🥳🥳

이제 증명이 거의 다 마무리 되었다. 우리가 증명하고자 한 것은 임의의 두 실수 $x$와 $y$에 대하여 $x < y$ 일 때 $x < p < y$를 만족시키는 유리수 $p$가 존재한다는 사실을 증명하고자 하였다. 내가 말하고 싶은 것은, $\frac{m}{n}$이 우리가 그토록 찾아다닌 $p$라는 사실이다.

$m$과 $n$은 정수이면서, $n$은 positive 이기 때문에 $0$이 아니므로 $\frac{m}{n}$은 당연히 유리수가 된다. 이것으로 증명은 완료된다. 그런데, 이 과정에서 나는 한 가지 의문이 들었었다. "$m$과 $n$이 서로소임을 보일 수가 있는가?" 에 대한 내용이었다.

$\sqrt{2}$가 무리수임을 증명하는 과정에서는 분모와 분자의 두 정수가 서로소임을 가정하였고, 그것이 모순을 발생시킴을 보였다. 그런데, 교재에서도 그렇고, 내가 생각해본 바에서도 $m$과 $n$이 서로소임을 보일 방법은 전혀 떠오르지 않았다. 결국 얻어낸 해답부터 말하자면, "서로소일 필요가 없다" 라는 점이다.

유리수의 표현 자체는 분모와 분자가 서로소여야 함을 강제하지 않는다. $\sqrt{2}$ 가 무리수임을 보이는 과정에서는 "서로소인 형태로도 나타낼 수 있고, 그렇게 나타낸 분모와 분자에 대하여" 이야기를 한 것이었다. 그렇기 때문에, 이 정리의 증명에서는 신경을 쓸 필요가 없었던 것이다. 그리고 이 의문이 해소된 시점에서, 증명은 끝나게 된다. $\blacksquare$

이로써 두 정리의 증명이 모두 마무리되었다. 본격적으로 나온 어려운 증명들이므로, 이해가 잘 가지 않는다면 시간을 들여 천천히, 여러 번, 직접 써보면서 이해해볼 것을 추천한다.

마무리

오늘 배운 내용들을 간단하게 요약해보겠다.

LUBP를 가진 ordered field 가 존재하며, 그걸 실수체라 부르고 $\mathbb{R}$ 이라고 쓴다.
실수체에서 성립하는 archimedean property 에 대해 알아보고 이를 증명하였다.
”$\mathbb{Q}$ is dense in $\mathbb{R}$” 이라고 불리는 정리에 대해 알아보고 이를 증명하였다.
내일은 실수의 또 다른 성질에 대해 하나 알아보고, 실수의 표기법인 “decimal”에 대해 알아보고, 확장된 실수 체계를 정의해보도록 하겠다.

오늘의 공부는 여기까지!

← Previous Post Next Post →